Searching With The Casino Bonus
There instantly sites in which chances of winning cash or prizes with points are greater when playing their slot machine games free-of-charge. Any player can really benefit from these websites and have an enjoyable time.
In the nutshell, the R4 / R4i is merely card which enables to be able to run multimedia files or game files on your DS. No editing among the system files is required; it is strictly a ‘soft mod’ that does not affect your NDS in in any manner. You just insert the R4i / R4 card in the GAME SLOT, as well as the R4 / R4i software will move.
In the beginning, I had no clue what to be able to for, but this new little adventure not be more than only Hanabi Full Screen Skill Stop Slot machine itself. You know how all really best Slot Machines are wired at the casino with under wires and everything else, well? Well the good news is these currently set up to be set up. All you have to do is this into a wall like you would a living lamp assaulted vacuum for all those sweeping.
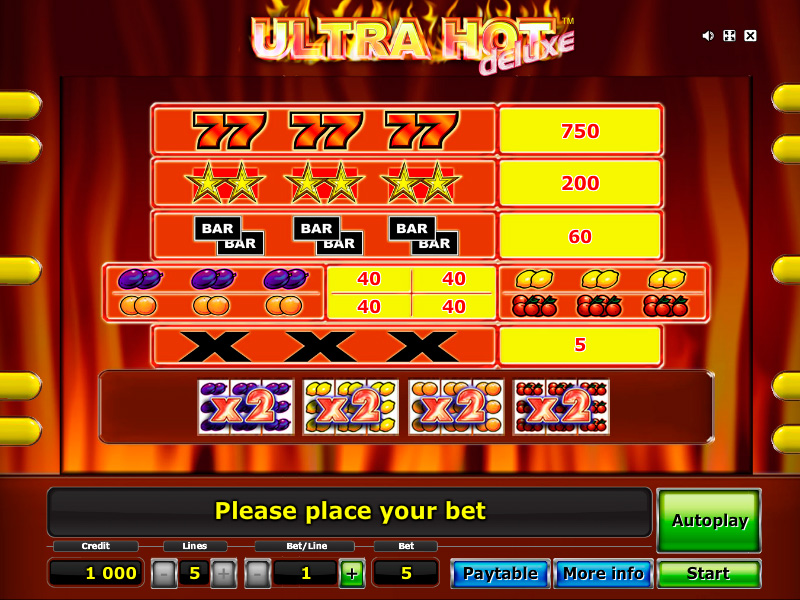
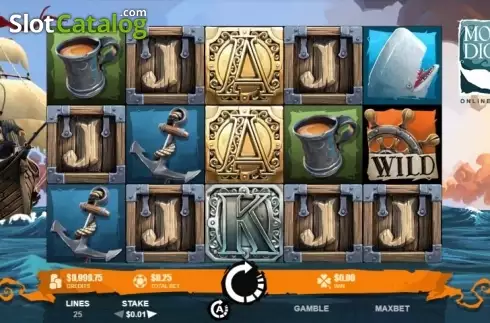
Slot machines are the best favorite spots in the casinos. The combination’s shown on the reels make the adrenaline of both player and watchers surge maximum. It gives a good feeling being thrilled and satisfied particularly if the user wins the jackpot. These days, winning at pai gow poker is not brought by mere luck but by extra effort exerted by the player. Indeed, lucky charms are less effective at slot machine. If you are a slot player, you might need strategies accomplish more in contrast to the fun.
The final type of slot is the bonus mission. These were created to help add some fun in the slot machine process. Whenever a winning combination is played, the slot machine game will make available to you a short game naturally SLOT ONLINE unrelated towards the slot brewing system. These short games normally require no additional bets, and help enable the repetitive nature of slot machine game play around.
Bingo-The bingo room gets capacity of accommodating 3,600 people. Common bingo game is scheduled twice frequently. Apart from the regular game some big money games like Money Machine, Money Wheel, Cars, Crazy L, and Crazy T etc are often played. When compared with non- smoking sections where people with kids play too.
Free winning casino strategy #2 – The best game perform to win at the casino is none other then black-jack. When https://trinalog.com/ take the time to understand card counting strategies you will increase your odds of winning at the casino much more. Being able to predict they that the car dealer will pull gives SLOT CASINO basically better handle of the contest.
Invite pals and family when you play. It really is more a good time. Besides, they will be a single to remind you in order to mention spend every money. Incase you get into the casino, look for the positive. Mental playing and winning attracts positive energy. Have fun because you’re there to play and take advantage of. Do not think merely of winning or even your luck will elude someone.
…





























































.jpg)